Consider the Las Vegas wheel problem in Example 1 where the wheel no longer has equal probabilities but probabilities for values $10, $6, $4, $0 as follows:

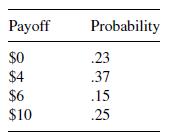
Consider three spins and decide your optimal strategy.

Data from example 1

You are in a Las Vegas Casino and have encountered the following game board, which is to be spun randomly (electronically):

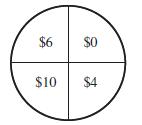
Assuming that each outcome is equally likely, you compute the possible payoffs and probabilities as:

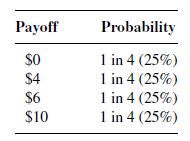
You have a maximum of 3 spins but may stop after either the first or the second spin and take the result of that spin. You have decided to play the game 100 times. Clearly, after the first spin, you would take $10 and stop, and you would spin again if you had $0. But, what about $4 and $6? And what is your criterion after the second spin? Clearly, after the third spin, if you get that far, you are stuck with whatever occurs. What you seek is an optimal decision strategy. That is: 

After spin 1, take?
After spin 2, take?
After spin 3, take anything.

If your goal is to maximize profit over the 100 games, what should you do? If you do want to make a profit, what is the maximum amount you should pay to play? To solve this problem, we start at the final spin and work our way backward. That is, if we know the monetary value of spin 3, we can decide what to do after spin 2. Of course, if we get to spin 3, we must take anything. Computing the expected value of spin 3, take anything, we have:

Interpreting
If we arrive at spin 3, we will average $5.00 on that final spin. Consequently, after spin 2 we should take any result greater than $5.00.

Now, we compute the expected value at the beginning of spin 2. We are going to take $10 or $6; otherwise, if we spin a $4 or $0, we will go to spin 3, which we now know is worth $5.00. Computing, we have:

If we expect to make $6.50 with spins 2 and 3 in front of us, then after spin 1 we should take only the $10. Summarizing, we have our optimal decision process that maximizes the expected value:

After spin 1, take $10 only.
After spin 2, take $10 or $6.
After spin 3, take anything.

While we have an optimal decision process, we still have not determined the value of the game. To do that, we must compute the expected value at spin 1, that is, with 3 spins in front of us. Since we take only the $10 outcome and otherwise go to spin 2, where we expect to make $6.50, we have:

If we play optimally, we will average $7.375. If we play the game a large number of times, say 100, we expect to make about $737.50 on average. If we pay more than $7.375 to play each game, we will lose money. Now, let's consider this process using a decision tree.