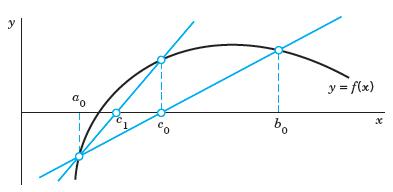
Figure 430 shows the idea. We assume that f is continuous. We compute the x-intercept c₀ of the line through (α₀,f(α₀)), (b₀, f(b₀)). If f(c₀) = 0, we are done. If f(α₀)f(c₀) < 0 (as in Fig. 430), we set α₁= α₀, b₁= c₀ and repeat to get c₁, etc. If f(α₀)f(c₀) > 0, then f(c₀)f(b₀) < 0 and we set α₁= c₀, b₁= b₀, etc.

(a) Show that

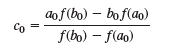
and write an algorithm for the method.

(b) Solve x⁴ = 2, cos x = √x, and x + ln x = 2, with α = 1, b = 2.

Transcribed Image Text:

aof (bo) – bo f(ao) f(bo) – f(ao) Co