Find the eigenvalues and eigenfunctions. Verify orthogonality. Start by writing the ODE in the form (1), using Prob. 6. Show details of your work.

Orthogonal polynomials play a great role in applications. For this reason, Legendre polynomials and various other orthogonal polynomials have been studied extensively. Consider some of the most important ones as follows.

(a) Chebyshev polynomials of the first and second kind are defined by

respectively, where n = 0, 1, · · · . Show that

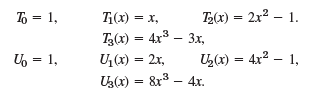
Show that the Chebyshev polynomials T_n(x) are orthogonal on the interval -1 ‰¤ x ‰¤ 1 with respect to the weight function r(x) = 1/ˆš1 - x². (To evaluate the integral, set arccos x = θ.) Verify that T_n(x), n = 0, 1, 2, 3, satisfy the Chebyshev equation

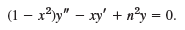
(b) Laguerre polynomials are defined by L₀ = 1, and

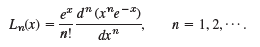
Show that

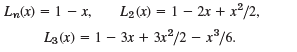
Prove that the Laguerre polynomials are orthogonal on the positive axis 0 ‰¤ x < ˆž with respect to the weight function r(x) = e^-x. Since the highest power in L_m is x^m, it suffices to show that ˆ«e^-xx^kL_n dx = 0 for k < n. Do this by k integrations by parts.

Data from Prob. 6

Show that y" + fy' + (g + λh) y = 0 takes the form (1) if you setp = exp (ˆ«f dx), q = pg, r = hp. Why would you do such a transformation?

Transcribed Image Text:

T, (x) = cos (n arccos x) sin [(n + 1) arccos x] = (x) "n VI - x? T, = 1, T;(x) = x, T(x) = 4x3 – 3x, U,(x) = 2x, Uz(x) = &r3 – 4x. T(x) = 2x2 – 1. %3D U, = 1, U(x) = 4x² – 1,