The idea is to get an equation from the vanishing of the determinant of a homogeneous linear system as the condition for a nontrivial solution in Cramer€™s theorem. We explain the trick for obtaining such a system for the case of a line L through two given points P₁: (x₁, y₁) and P₂: (x₂, y₂). The unknown line is αx + by = -c, say. We write it as αx + by + c · 1 = 0. To get a nontrivial solution a, b, c, the determinant of the €œcoefficients€ x, y, 1 must be zero. The system is

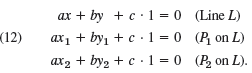
(a) Line through two points. Derive from D = 0 in (12) the familiar formula

(b) Find the analog of (12) for a plane through three given points. Apply it when the points are (1, 1, 1), (3, 2, 6), (5, 0, 5).

(c) Find a similar formula for a circle in the plane through three given points. Find and sketch the circle through (2, 6), (6, 4), (7, 1).

(d) Find the analog of the formula in (c) for a sphere through four given points. Find the sphere through (0, 0, 5), (4, 0, 1) , (0, 4, 1), (0, 0, -3) by this formula or by inspection.

(e) Find a formula for a general conic section (the vanishing of a determinant of 6th order). Try it out for a quadratic parabola and for a more general conic section of your own choice.

+ by + c 1-0 (Line L) %3D (12) , + byj + c .1 3D0 (R on L) + c -1%3D0 (, on L). + byz (P, on L). ] X1 - X2 1 2'