Determine the variables on which a pendulum's amplitude (or sometimes called the pendulum position) depends (see Fig.

Question:

Determine the variables on which a pendulum's amplitude (or sometimes called the pendulum position) depends (see Fig. 11.2). Use the Buckingham $\pi$ theorem; the relevant dimensional variables can be listed as pendulum's mass $(m)$, length of the rigid rod $(l)$, pendulum's period $(\tau)$, time $(t)$, gravitational acceleration $(g)$, and initial position of the pendulum $\left(\phi_{0}=\phi(0)ight)$.

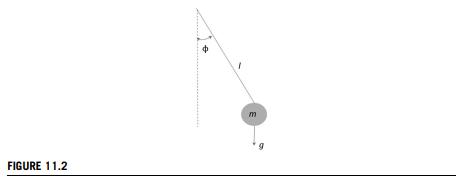
FIGURE 11.2 m