(a) Let D be an integral domain and c D. Let (x) and (x - c)...

Question:

(a) Let D be an integral domain and c ϵ D. Let ∫(x) 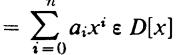and ∫(x - c) = 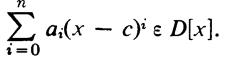Then f(x) is irreducible in D[x] if and only ∫(x - c) is irreducible.

(b) For each prime p, the cyclotomic polynomial ∫ = x^p-1 + x^P-2 + • • • + x + 1 is irreducible in Z[x).

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Algebra Graduate Texts In Mathematics 73

ISBN: 9780387905181

8th Edition

Authors: Thomas W. Hungerford

See More Books

Question Posted: Apr 15, 2023 03:05 AM

See More Questions

(a) If D is an integral domain and c is an irreducible element in D, then D[x] is not a principal ideal domain. (b) Z[x] is not a principal ideal domain. (c) If F is a field and n 2, then F[x 1 ,...
Find all the second partial derivatives of the function b) f(x,y) = ln(3x + 5y). %3D
Let E be a finite extension field of F. Let D be an integral domain such that F D E. Show that D is a field.
Define the term CHAMPERTY
Give an example of transitory income. What effect does this income have on the marginal propensity to consume?
Four sales representatives for a company are to be chosen at random to participate in a training program. The company has eight sales representatives, two in each of four regions. What is the...
INTEL: Building Blocks Inside Out Visit www.pearsonglobaleditions.com/malhotra to read the video case and view the accompanying video. Intel: Building Blocks Inside Out demonstrates the critical role...
Quansi, Inc., reported the following on the company's income statement in 2012 and 2011: a. Determine the number of times interest charges were earned for 2011 and 2012. Round to one decimal place....
Public Company acquired the net assets of Sun Company by paying cash $420,000. At that time, the book value of the net assets of Sun Company was $300,000 and the fair value its net assets was...
Question A: Stay Safe International manufactures industrial safety equipment at its plant in Evans- ville, Indiana. The company has initiated DRP to coordinate finished goods distribution from the...
Let R be a ring with identity and S the ring of all n X n matrices over R. J is an ideal of S if and only if J is the ring of all n X n matrices over I for some ideal I in R.
Let have degree n. Suppose that for some k (0 n ; p a k ; p| a i for all O i k - 1; and p 2 a 0 Show that has a factor g of degree at least k that is irreducible in Z[x]. [= ax Z[x] i-0
Alicia has been working for JMM Corp. for 32 years. Alicia participates in JMM's defined benefit plan. Under the plan, for every year of service for JMM she is to receive 2percent of the average...
How strong must an electric field in a metal be in order for electrons in the field to have a drift speed of $10 \mathrm{~mm} / \mathrm{s}$ if the time interval between electron-ion collisions is...
Air enters a pipe $(f=0.02)$ of diameter $0.05 \mathrm{~m}$ with stagnation pressure and temperature equal to $1 \mathrm{MPa}$ and $300 \mathrm{~K}$, respectively. The pipe exhausts into the ambient...
A copper wire that is $600 \mathrm{~mm}$ long and has a radius of $1.0 \mathrm{~mm}$ is connected to the terminals of a $9.0-\mathrm{V}$ battery. What is the current through the wire...
Air enters a $3 \mathrm{~m}$ long pipe $(f=0.02)$ of diameter $0.025 \mathrm{~m}$ at a stagnation temperature of $300 \mathrm{~K}$. If the static pressure of the air at the exit of the pipe is $100...
You want to use a length of insulated rigid metal rod to discharge the plates of a parallel-plate capacitor without allowing the electric field in the rod to exceed 1000 N/C. The area $A$ of each...
Morris Zapp and Philip Swallow consume wine and books. Morris has an initial endowment of 60 books and 10 bottles of wine. Philip has an initial endowment of 20 books and 30 bottles of wine. They...
QUESTION 9 HC-O-C-R R-C-O-CH HC-O-P-O-CH-CH-NH3* O || O a. Phosphatidic acid, Serine O b. Lysophosphatidic acid, Serine, Free FA O c. Lysophosphatidylserine, Free FA O d. 2 Free FAs, Serine, Glycerol...
Carry out the test in Problem 7.38 using the critical value method with an level of .05, and summarize your findings? The standard deviation of daily iron intake in the larger population of 9- to...
What is the p-value for the test conducted in Problem 7.39? The standard deviation of daily iron intake in the larger population of 9- to 11-year-old boys was 5.56 mg. We want to test whether the...
Compute a 95% CI for the underlying variance of daily iron intake in the low-income group. What can you infer from this CI? The standard deviation of daily iron intake in the larger population of 9-...
The computer workstation furniture manufacturing that Santana Rey started is progressing well. As of the end of June, Business Solutions's job cost sheets show the following total costs accumulated...
Mason Company provided the following data for this year: Sales Direct labor cost Raw material purchases Selling expenses Administrative expenses Manufacturing overhead applied to work in process...
Santana Rey, owner of Business Solutions, diversifies her business by also manufacturing computer workstation furniture. Required: 1. Classify the following manufacturing costs of Business Solutions...

(a) Let D be an integral domain and c D. Let (x) and (x - c)...

Question:

|| Σ_aix* eD[x] i=()

Step by Step Answer:

a To prove the statement we need to show that if fx is irreducible in Dx then x c is irreducible and ...View the full answer

Algebra Graduate Texts In Mathematics 73

Students also viewed these Mathematics questions