Lagrange's Interpolation Formula. If F is a field, a₀,a₁, ... , a_n are distinct elements of F and c₀,c₁, ... , C_n are any elements of F, then 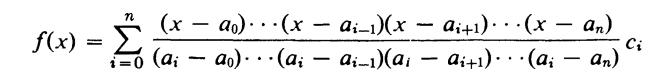is the unique polynomial of degree ≤ n in F[x] such that ∫(a_i) = C_i for all i [see Exercise 11].

Data from exercise 11

If c_o, c₁, ... , C_n are distinct elements of an integral domain D and d_o, ... , d_n are any elements of D, then there is at most one polynomial ∫ of degree ≤ n in D[x] such that ∫(c_i) = d_i for i = 0, 1, ... ,n. [For the existence of ∫.

Transcribed Image Text:

f(x) = n i=0 (a; - ao)...(x ao) (ai . .. - ai_1)(x ai_1)(ai - - ai+1)(x - ai+1)(a; · - An) Ci an)