Use the Krull-Schmidt Theorem to prove Theorems 2.2 and 2.6 (iii) for finite abelian groups. Data From
Question:
Use the Krull-Schmidt Theorem to prove Theorems 2.2 and 2.6 (iii) for finite abelian groups.
Data From Theorem 2.2
Every finitely generated abe/ian group G is (isomorphic to) a finite direct sum of cyclic groups, each of which is either infinite or of order a power of a prime.
SKETCH OF PROOF.
The theorem is an immediate consequence of Theorem 2.1 and the following lemma. Another proof is sketched in Exercise 4.
Data From Theorem 2.6
Let G he a finitely generated abelian group.(i) There is a unique nonnegative integer s such that the number of infinite cyclic summands in any decomposition of G as a direct sum of cyclic groups is precisely s;(ii) either G is free abelian or there is a unique list of (not necessarily distinct) positive integers m1, ... , mt such that m1 > 1, m1| m2|· · · |mt and![]()
with F free abelian;(iii) either G is free abelian or there is a list of positive integerl P181 , ••• , Pk8k, which is unique except for the order of its members, such that p1, ... , Pk are (not necessarily distinct) primes, s1, ... , sk are (not necessarily distinct) positive integers and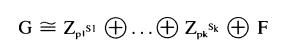
with F free abelian.
PROOF.
(i) Any decomposition of Gas a direct sum of cyclic groups (and there is at least one by Theorem 2 .1) yields an isomorphism G ≅ H⊕F, where H is a direct sum of finite cyclic groups (possibly 0) and Fis a free abelian group whose rank is precisely the number s of infinite cyclic summands in the decomposition. If L : H → H⊕F is the canonical injection (h |→ (h,0)), then clearly ,L(H) is the torsion subgroup of H⊕F. By Lemma 2.5, Gt ≅L(H) under the isomorphism G ≅ H⊕F. Consequently by Corollary 1.5.8, G/Gt ≅ (F⊕H)/L(H) ≅ F. Therefore, any decomposition of G leads to the conclusion that G/Gt, is a free abelian group whose rank is the numbers of infinite cyclic summands in the decomposition. Since G/Gt, does not depend on the particular decomposition and the rank of G/Gt is an invariant by Theorem 1.2, s is uniquely determined.(iii) Suppose G has two decompositions, say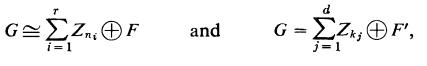
Step by Step Answer:

Algebra Graduate Texts In Mathematics 73
ISBN: 9780387905181
8th Edition
Authors: Thomas W. Hungerford




