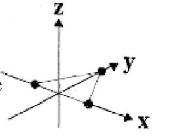
For the group of an equilateral triangle, let operation A be a "flip" a rotation by \(180^{\circ}\) about the \(y\)-axis. Show that \(\phi_{1}=x^{2}-y^{2}\) and \(\phi_{2}=y z\) are basis functions for \(\mathbf{A}\) by finding the corresponding matrix representation for \(\mathbf{A}\).

Transcribed Image Text:

N4 y