In our example of the free-falling bungee jumper, we assumed that the acceleration due to gravity was a constant value of 9.81 m/s². Although this is a decent approximation when we are examining falling objects near the surface of the earth, the gravitational force decreases as we move above sea level. A more general representation based on Newton’s inverse square law of gravitational attraction can be written as

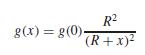
where g(x) = gravitational acceleration at altitude x (in m) measured upward from the earth’s surface (m/s²), g(0) = gravitational acceleration at the earth’s surface (∼= 9.81 m/s²), and R = the earth’s radius (∼= 6.37 × 10⁶ m).
(a) In a fashion similar to the derivation of Eq. (1.8), use a force balance to derive a differential equation for velocity as a function of time that utilizes this more complete representation of gravitation. However, for this derivation, assume that upward velocity is positive.

Equation 1.8

(b) For the case where drag is negligible, use the chain rule to express the differential equation as a function of altitude rather than time. Recall that the chain rule is

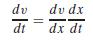
(c) Use calculus to obtain the closed form solution where v = ν₀ at x = 0.
(d) Use Euler’s method to obtain a numerical solution from x = 0 to 100,000 m using a step of 10,000 m where the initial velocity is 1500 m/s upward. Compare your result with the analytical solution.

Transcribed Image Text:

R² (R+ x)² g(x) = g(0)-