Suppose that a spherical droplet of liquid evaporates at a rate that is proportional to its surface area.

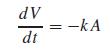
where V = volume (mm³), t = time (min), k = the evaporation rate (mm/min), and A = surface area (mm²). Use Euler’s method to compute the volume of the droplet from t = 0 to 10 min using a step size of 0.25 min. Assume that k = 0.08mm/min and that the droplet initially has a radius of 2.5 mm. Assess the validity of your results by determining the radius of your final computed volume and verifying that it is consistent with the evaporation rate.

Transcribed Image Text:

-KA = ¹P ДР