A process has a target of μ 0 = 100 and a standard deviation of Ï = 4. Samples of size n = 1 are

A process has a target of μ₀= 100 and a standard deviation of σ = 4. Samples of size n = 1 are taken every two hours. Use Table 15-10.

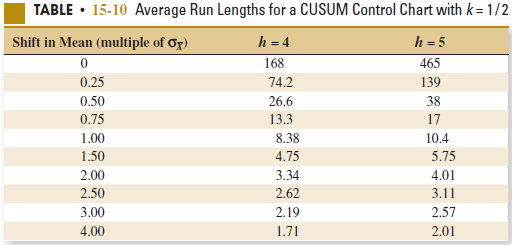
(a) Suppose that the process mean shifts to μ = 102. How many hours of production occur before the process shift is detected by a CUSUM with h = 5 and k = 1 / 2?

(b) It is important to detect the shift defined in part (a) more quickly. A proposal to reduce the sampling frequency to 0.5 hour is made. How does this affect the CUSUM control procedure? How much more quickly is the shift detected?

(c) Suppose that the 0.5 hour sampling interval in part (b) is adopted. How often do false alarms occur€™s with this new sampling interval? How often did they occur with the old interval of two hours?

(d) A proposal is made to increase the sample size to n = 4 and retain the two-hour sampling interval. How does this suggestion compare in terms of average detection time to the suggestion of decreasing the sampling interval to 0.5 hour?

Table 15-10

TABLE 15-10 Average Run Lengths for a CUSUM Control Chart with k= 1/2 Shift in Mean (multiple of Og) h = 4 h = 5 168 465 0.25 74.2 139 26.6 0.50 38 0.75 13.3 17 10.4 1.00 8.38 1.50 4.75 5.75 2.00 3.34 4.01 2.50 2.62 3.11 2.19 3.00 2.57 4.00 1.71 2.01