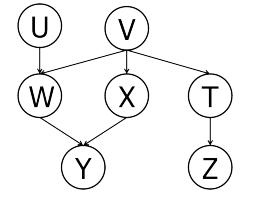
a. For the Bayes net in Figure S13.37, we are given the query P(Z | + y). All variables are Boolean. Assume we run variable elimination to compute the answer to this query, with the following variable elimination ordering: U, V , W, T, X. After inserting evidence, we have the following factors to start out with:

P(U), P(V ), P(W |U, V ), P(X | V ), P(T | V ), P(+y | W, X), P(Z | T) . 

When eliminating U we generate a new factor f1 as follows: 

f₁(V, W) = Σ_u P(u)P(W | u, V ) .

This leaves us with the factors:

P(V ), P(X | V ), P(T | V ), P(+y | W, X), P(Z | T), f₁(V, W) .

Now complete the remaining steps: 

(i) When eliminating V we generate a new factor f₂ as follows: 

(ii) This leaves us with the factors: 

(iii) When eliminating W we generate a new factor f₃ as follows: 

(iv) This leaves us with the factors: 

(v) When eliminating T we generate a new factor f₄ as follows: 

(vi) This leaves us with the factor: 

(vii) When eliminating X we generate a new factor f₅ as follows: 

(viii) This leaves us with the factor: 

b. Briefly explain how P(Z | + y) can be computed from f₅.

c. Amongst f₁, f₂, . . . , f₅, which is the largest factor generated? How large is this factor? 

d. Find a variable elimination ordering for the same query, i.e., for P(Z | y), for which the maximum size factor generated along the way is smallest.

Figure S13.37

Transcribed Image Text:

U (W) Y V X T (Z) N