Consider a naive Bayes classifier with two features, shown below We have prior information that the probability model can be parameterized by and p, as shown below We have a training set that contains all of the following n 000 examples with X 1 0, X 2 0, Y 0 n 010 examples with X 1 0, X 2 1, Y 0 n...

a We first write down the likelihood of the training data T Y X 1 X 2 We then take the logarithm o ...

Consider a naive Bayes classifier with two features, shown below. We have prior information that the probability

Question:

Consider a naive Bayes classifier with two features, shown below. We have prior information that the probability model can be parameterized by λ and p, as shown below:

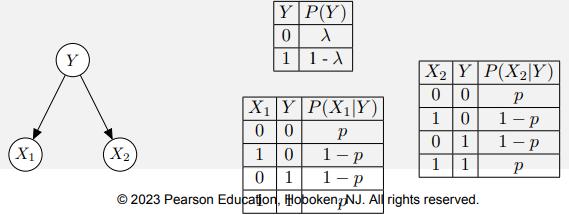
We have a training set that contains all of the following:

• n₀₀₀ examples with X₁ = 0, X₂ = 0, Y = 0

• n₀₁₀ examples with X₁ = 0, X₂ = 1, Y = 0

• n₁₀₀ examples with X₁ = 1, X₂ = 0, Y = 0

• n₁₁₀ examples with X₁ = 1, X₂ = 1, Y = 0

• n₀₀₁ examples with X₁ = 0, X₂ = 0, Y = 1

• n₀₁₁ examples with X₁ = 0, X₂ = 1, Y = 1

• n₁₀₁ examples with X₁ = 1, X₂ = 0, Y = 1

• n₁₁₁ examples with X₁ = 1, X₂ = 1, Y = 1

a. Solve for the maximum likelihood estimate (MLE) of the parameter p with respect to n₀₀₀, n₁₀₀, n₀₁₀, n₁₁₀, n₀₀₁, n₁₀₁, n₀₁₁, and n₁₁₁.

b. For each of the following values of λ, p, X₁, and X₂, classify the value of Y

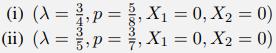
c. Now let’s consider a new model M2, which has the same Bayes’ Net structure as M1, but where we have a p₁ value for P(X₁ = 0 | Y = 0) = P(X₁ = 1 | Y = 1) = p₁ and a separate p₂ value for P(X₂ = 0 | Y = 0) = P(X₂ = 1 | Y = 1) = p₂, and we don’t constrain p₁ = p₂. Let L_M1 be the likelihood of the training data under model M₁ with the maximum likelihood parameters for M₁. Let L_M₂ be the likelihood of the training data under model M₂ with the maximum likelihood parameters for M2. Are we guaranteed to have L_M1 ≤ L_M₂?