You are an exobiologist, studying the wide range of life in the universe. You are also an avid dancer and have an excellent model of the way species invent dancing. The key variables are:

Sound sensing (S): Whether or not a species has the ability to sense sound Cold climate (C): Whether or not the native planet of the species has cold weather Music (M): Whether or not the species invented music Non-verbal communication (N): Whether or not the species has any form of non-verbal communication You model the relationships between these variables and dancing (D) using the Bayes net specified in Figure S13.48.

You want to know how likely it is for a dancing, sound-sensing species to invent music, according to this Bayes net. You decide to do inference via sampling. You use prior sampling to draw the samples in Figure S13.48. 

a. Based on rejection sampling using the samples above, what is the answer to your query P(−m | +d, +s)?

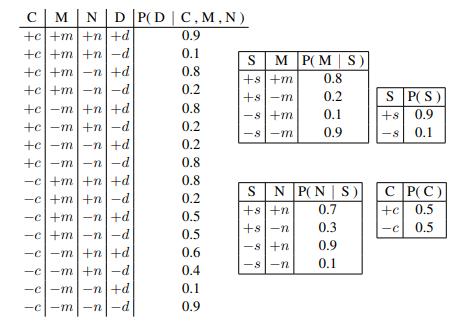
While your sampling method has worked fairly well in many cases, for rare cases (like species that can’t sense sound) your results are less accurate as rejection sampling rejects almost all of the data. You decide to use likelihood weighting instead. The conditional probabilities of the Bayes net are listed in Figure S13.49.

You now wish to compute the probability that a species that has no sound-sensing (−s) or dancing (−d) nonetheless has music (+m), using likelihood weighting. I.e., you want P(+m | −s, −d). 

b. You draw the samples in Figure S13.48, using likelihood weighting. For each of these samples, indicate its weight.

c. Compute the answer to your query, P(+m | −s, −d), using likelihood weighting with these samples.

Figure S13.48

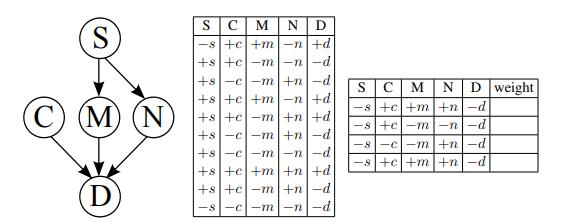
Figure S13.49

Transcribed Image Text:

S C (M) (N) D S C M N D -8+c+m-n+d +8+c-m-n-d +8-c-m+n-d +8+c+m-n+d +8+cm+n+d +s-c-m+n-d +8-c-m-n-d +8+c+m+n +d +8+cm+n-d -8-c-m-n-d SCMND weight -8+c+m+n-d -8+c-m-n-d -8-c-m+n-d -8+c+m+n-d