This exercise is about partizan games as treated in Section 1.8.

(a) Complete the proof of (1.32) by showing that Right as starting player loses.

The partizan game (Black-White) Hackenbush is played on a figure consisting of nodes and black or white edges that are connected to these nodes or to the ground, as in the pictures below. In a move the Left player removes a black edge and the Right player a white edge; if no such edge exists then the player loses. After such a move, all nodes and edges no longer connected to the ground disappear as well. For example, in a Hackenbush figure with a white edge on top of a black edge, Left can remove the bottom (black) edge and creates the zero game, whereas Right can remove the top (white) edge and leaves a single black edge.

(b) Recall that for a combinatorial game \(G\) its negative is a game \(-G\) so that \(G+(-G) \equiv 0\). Describe the negative of a Hackenbush figure, and give an example. [Hint: Compare (1.24).]
We consider Hackenbush stalks, which are just paths of edges of either color. It can be shown that any such stalk is a number, with some examples considered here.

(c) Draw the game that represents the number 3 (where Left is 3 moves ahead).

(d) Find the numbers represented by the following Hackenbush stalks. Justify your answers. It helps to study and understand (1.36), and to consider only undominated moves of the players; also, compare the strength of the Left (black) player for these games to get an idea about the answer: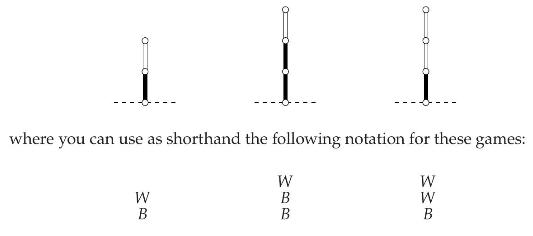

(e) Construct a Hackenbush game (preferably a single stalk) that represents the number \(\frac{7}{4}\).

Transcribed Image Text:

Left 1 Right