The impartial game Gray Hackenbush is played on a figure consisting of nodes and edges that are connected to these nodes or to the ground (the ground is the dashed line in the pictures below). A move is to remove an edge, and with it all the edges that are then no longer connected to the ground. For example, in the leftmost figure below, one can remove any edge in one of the three stalks. Removing the second edge from the stalk that consists of three edges takes the topmost edge with it, leaving only a single edge. All edges are colored gray, which means they can be removed by either player, so this is an impartial game. As usual, players alternate and the last player able to move wins.

(a) Compute the Nim values for the following three Gray Hackenbush figures (using what you know about Nim, and the mex rule):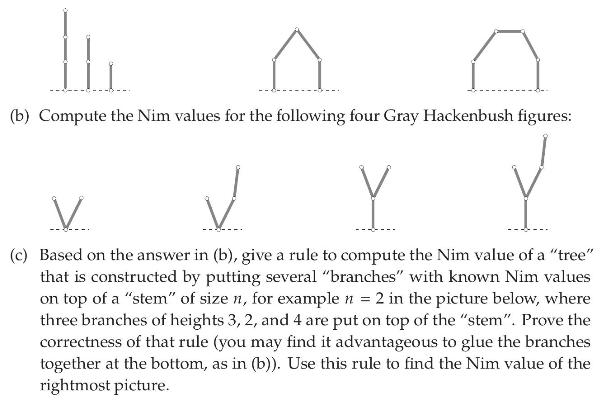

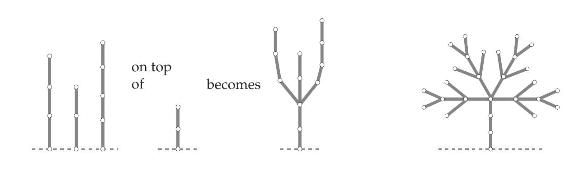
(b) Compute the Nim values for the following four Gray Hackenbush figures: V Y (c) Based on the answer in (b), give a rule to compute the Nim value of a "tree" that is constructed by putting several "branches" with known Nim values on top of a "stem" of size n, for example n = 2 in the picture below, where three branches of heights 3, 2, and 4 are put on top of the "stem". Prove the correctness of that rule (you may find it advantageous to glue the branches together at the bottom, as in (b)). Use this rule to find the Nim value of the rightmost picture.