A cubic Bezier curve is defined by four points (P₀ through P₃) from the parametric equations given by (1 − t)³P₀ + 3(1 − t)² tP₁ + 3(1 − t)t²P₂ + t³P₃, 3 where 0 ≤ t ≤ 1. Note that the points P₀ through P₃ are multiplied by terms of the binomial expansion [(1 − t) + t]³. Using a similar process, find the equation of the fourth-degree Bezier curve defined by the five points P₀ through P₄. (see Example 6 in Section 15.3).

Data from Example 6 in Section 15.3.

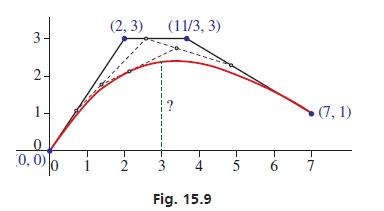
Bezier curves are used frequently in computer graphics to generate smooth curves and surfaces. In particular, cubic Bezier curves are formed by four points, two that define the curve’s start and end (at t = 0 and t = 1) and two that “stretch” the middle part of the graph. The red curve in Fig. 15.9 shows a Bezier curve design for the roofline of a new art museum. It is defined by the parametric equations shown below, where the units for x and y are in tens of feet.

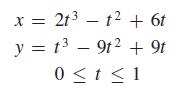
Find the height of the roofline at the point that is 30 ft to the right of the left edge. To find this height, we will substitute 3 for x in the top parametric equation, solve for t, and then substitute the result into the bottom equation to find y.

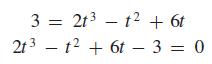
If the above equation has any rational roots, they must be of the form

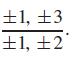
Since we know 0 ≤ t ≤ 1, the only possibilities are t = 1/2 or t = 1. We also know that t = 1 represents an endpoint, so it is not the solution we desire. Thus, we will try t = 1/2 (orn0.5) using synthetic division.

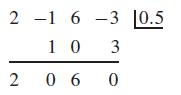
Since the remainder is zero, t = 0.5 is a root (the quotient 2x² + 6 indicates that the other roots are not real numbers). To find the value of y, we substitute t = 0.5 into the second parametric equation:
y = (0.5)³ − 9(0.5)² + 9(0.5) = 2.375

Therefore, y = 2.375 (in tens of ft.), which means the height of the roofline is 23.75 ft at the desired location.

Transcribed Image Text:

x = y = 2t³t² t³ 13 0 ≤ t ≤ 1 + 6t 9t² + 9t