Consider the following stochastic shortest route problem over a three-period planning horizon for the network shown below: 

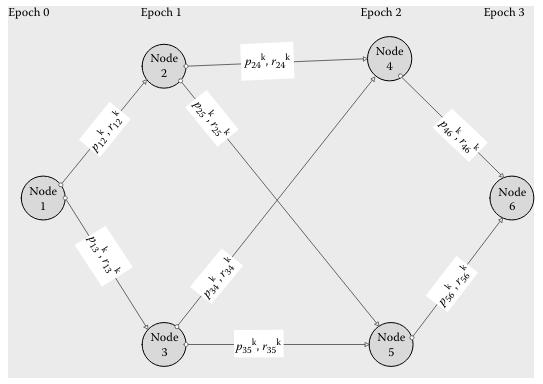
The network has six nodes numbered 1 through 6. One time period is needed to traverse an arc between two adjacent nodes. The origin, node 1, is entered at epoch 0. Nodes 2 and 3 can be reached at epoch 1 in one step from node 1 by traversing arcs (1,2) and (1, 3), respectively. Nodes 4 and 5 can be reached at epoch 2 in one step from node 2 by traversing arcs (2, 4) and (2, 5), respectively. Nodes 4 and 5 can also be reached at epoch 2 in one step from node 3 by traversing arcs (3, 4) and (3, 5), respectively. The final destination, node 6, can be reached at epoch 3 in one step from nodes 4 and 5 by traversing arcs (4, 6) and (5, 6), respectively. The network has no cycles. That is, once a node has been has been reached, it will not be visited again. A decision k at a node i identifies the node k chosen to be reached at the next epoch. The network is stochastic because a decision k made at a node i can result in the process moving to another node instead of the one chosen. Also, the distance, or arc length, between adjacent nodes is a function of the decision made at the current node. The objective is to find a path of minimum expected length from node 1, the origin, to node 6, the final destination.

To model this network problem as an MDP, the following variables are defined.

is the expected distance from node i to node j when decision k is made at node i at epoch n. 

The network is Markovian because the node j reached at epoch n+1 depends only on the present node i and the decision k made at epoch n. The transition probabilities and the actual distances corresponding to the decisions made at every node are shown in the table below. Transition probabilities and actual distances for stochastic shortest route problem.

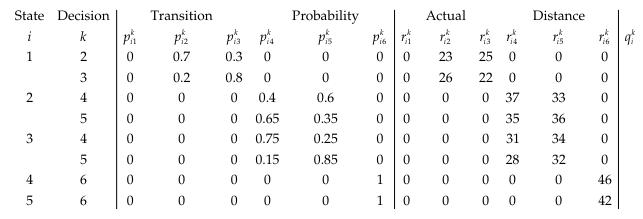
(a) Calculate the expected distances q_i^k from node i to node j when decision k is made at every node i at epoch n.

(b) Model this stochastic shortest route problem as a unichain MDP.

(c) Use value iteration to find a path of minimum expected length from node 1, the origin, to node 6, the final destination, over a 3 day planning horizon.

Transcribed Image Text:

Epoch 0 Epoch 1 Node P1212- P1313 Node 2 Node P25, 25 k P3434 k P24 k 24 Epoch 2 Node 4 Epoch 3 P3535 Node: 5 P46 46 Node 6