Regression through the origin. Sometimes it is known from theoretical considerations that the straight-line relationship between two variables x and y passes through the origin of the xy-plane. Consider the relationship between the total weight y of a shipment of 50-pound bags of flour and the number x of bags in the shipment. Since a shipment containing x = 0 bags (i.e., no shipment at all) has a total weight of y = 0, a straight-line model of the relationship between x and y should pass through the point x = 0, y = 0. In such a case, you could assume that b0 = 0 and characterize the relationship between x and y with the following model:

The least squares estimate of b1 for this model is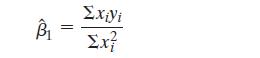

From the records of past flour shipments, 15 shipments were randomly chosen and the data shown in the following table were recorded.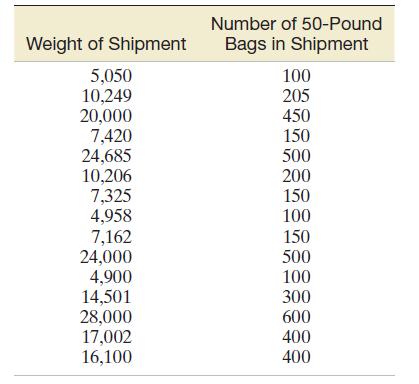

a. Find the least squares line for the given data under the assumption that b0 = 0. Plot the least squares line on a scatterplot of the data.

b. Find the least squares line for the given data, using the model

(i.e., do not restrict b0 to equal 0). Plot this line on the same scatterplot you constructed in part a.

c. Refer to part

b. Why might b n 0 be different from 0 even though the true value of b0 is known to be 0?

d. The estimated standard error of b n 0 is equal to

to test the null hypothesis H0: b0 = 0 against the alternative Ha: b0 0. Take a = .10. Should you include b0 in your model?

Transcribed Image Text:

y = x +