The relevance of variance and covariance developed for random variables in this chapter carries over to the
Question:
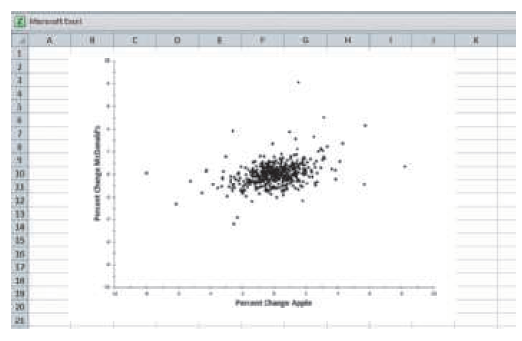
Motivation
(a) An investor is considering buying stock in Apple and McDonald€™s. Explain to the investor, in nontechnical language, why it makes sense to invest in both companies rather than investing in just one or the other.
Method
(b) Why is the Sharpe ratio useful for comparing the performance of two stocks whose values don€™t have the same variances?
(c) Based on the observed sample correlation in these data, does it appear sensible to model percentage changes in the values of these stocks as independent?
Mechanics
(d) Find the Sharpe ratio for a daily investment in Apple, in McDonald€™s, or equally split between Apple and McDonald€™s. Use the same risk-free rate as in the text (0.015). Which choice seems best?
(e) Form a new column in the data that is the average of the columns with the percentage changes for Apple and McDonald€™s. Find the mean and SD of this new variable and compare these to the values found in part (d).
(f) Find the Sharpe ratio for an investment that puts three-quarters of the money into McDonald€™s and one-quarter into Apple. Compare this combination to the mix considered in part (d). Which looks better?
Message
(g) Explain your result to the investor. Does it matter how the investor divides the investment between the two stocks?
Stocks or shares are generally equity instruments that provide the largest source of raising funds in any public or private listed company's. The instruments are issued on a stock exchange from where a large number of general public who are willing...
Step by Step Answer:
a A high expected return may not be attractive if the investment ...View the full answer
Statistics For Business Decision Making And Analysis
ISBN: 9780134497167
3rd Edition
Authors: Robert A. Stine, Dean Foster
