There is an urn containing 9 balls, which can be either green or red. The number of red balls in the urn is not known. One ball is drawn at random from the urn, and its color is observed.
(a) What is the Bayesian universe of the experiment.
(b) Let \(X\) be the number of red balls in the urn. Assume that all possible values of \(X\) from 0 to 9 are equally likely. Let \(Y_{1}=1\) if the rst ball drawn is red, and \(Y_{1}=0\) otherwise. Fill in the joint probability table for \(X\) and \(Y_{1}\) given below:

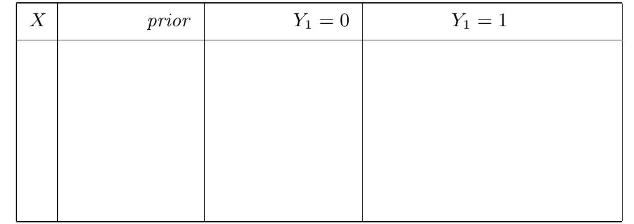
(c) Find the marginal distribution of \(Y_{1}\) and put it in the table.
(d) Suppose a red ball was drawn. What is the reduced Bayesian universe?
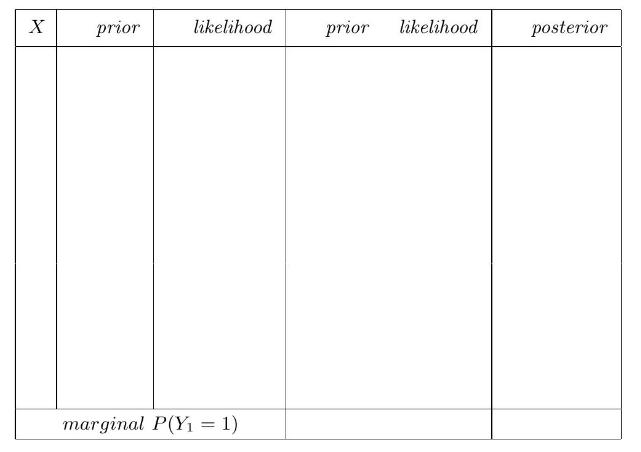
(e) Calculate the posterior probability distribution of \(X\).
(f) Find the posterior distribution of \(X\) by filling in the simplified table:

Transcribed Image Text:

X prior Y = 0 Y = 1