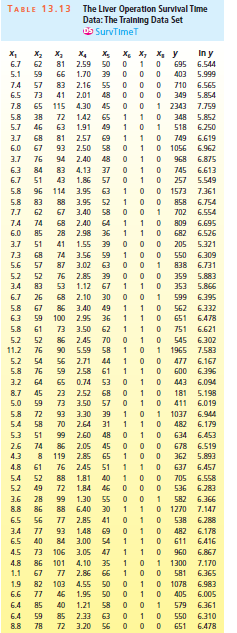
When developing a regression model to predict a dependent variable y, it is best, if there are enough data, to €œbuild€ the model using one data set (called the training data set) and then €œvalidate€ the model by using it to analyze a different data set (called the validation data set). To illustrate this, Kutner, Nachtsheim, Neter, and Li (2005) consider 108 observations described by the dependent variable y = survival time (in days) after undergoing a particular liver operation and the independent variables x₁= blood clotting score, x₂= prognostic index, x₃= enzyme function test score, x₄= liver function test score, x₅= age (in years), x₆= 1 for a female patient and 0 for a male patient, x₇= 1 for a patient who is a moderate drinker and 0 otherwise, and x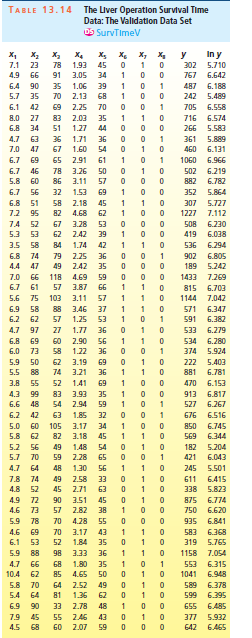₈= 1 for a patient who is a heavy drinker and 0 otherwise. Because 108 observations are a fairly large number of observations, Kutner and his fellow authors randomly divided these observations into two equal halves, obtaining the training data set in Table 13.13 and the validation data set in Table 13.14. In the exercises of Section 14.10 of Chapter 14 the reader will use both data sets to develop a multiple regression model that can be used to predict survival time, y, for future patients. As a preliminary step in doing this, (1) Use the training data set to plot y versus each of x₁, x₂, x₃, and x₄, and (2) Use the training data set to plot ln y versus each of x₁, x₂, x₃, and x₄. (3) By comparing the two sets of data plots, determine whether the y values or the ln y values seem to exhibit more of a straight-line appearance and more constant variation as x₁, x₂, x₃, and x₄increase.

Transcribed Image Text:

TABLE 13.13 The Liver Operation Survival Time Data: The Tralning Data Set OS SurvTimet In y 6.544 х, х, х X4 х. 2.59 х, х, х, у 6.7 62 81 50 695 5.1 59 66 1.70 39 403 5.999 7.4 57 83 2.16 55 710 6.565 6.5 73 41 2.01 48 349 5.854 7.8 65 115 4.30 45 2343 7.759 5.8 38 72 1.42 65 348 5.852 5.7 46 63 1.91 49 518 6.250 3.7 68 81 2.57 69 749 6.619 O 1056 2.50 6.0 67 93 58 6.962 3.7 76 94 2.40 48 968 6.875 6.3 84 83 4.13 37 745 6.613 5.549 6.7 51 43 1.86 57 257 5.8 96 114 3.95 63 1573 7.361 5.8 83 88 3.95 52 858 6.754 3.40 7.7 62 67 58 702 6.554 7.4 74 68 2.40 64 809 6.695 6.0 85 28 2.98 36 682 6.526 3.7 51 41 1.55 39 205 5.321 7.3 68 74 3.56 59 550 6.309 5.6 57 87 3.02 63 838 6.731 5.2 52 76 2.85 39 359 5.883 1.12 3.4 83 53 67 353 5.866 6.7 26 68 2.10 30 599 6.395 5.8 67 86 3.40 49 562 6.332 6.3 59 100 2.95 36 651 6.478 5.8 61 73 3.50 62 751 6.621 5.2 52 86 2.45 70 545 6.302 11.2 5.59 1 1965 76 90 58 7.583 5.2 54 56 2.71 44 477 6.167 5.8 76 59 2.58 61 600 6.396 0.74 6.094 3.2 64 65 53 443 8.7 45 23 2.52 68 181 5.198 5.0 59 73 3.50 57 411 6.019 OE'E 39 31 1037 5.8 72 93 6.944 5.4 58 70 2.64 482 6.179 5.3 51 99 2.60 48 634 6.453 2.6 74 86 2.05 45 678 6.519 4.3 119 2.85 65 362 5.893 4.8 61 76 2.45 51 637 6.457 5.4 52 88 1.81 40 705 6.558 6.283 5.2 49 72 1.84 46 536 3.6 28 99 1.30 55 582 6.366 8.8 86 88 6.40 30 1270 7.147 6.5 56 77 2.85 41 538 6.288 3.4 77 93 1.48 69 482 6.178 6.5 40 84 3.00 54 611 6.416 6.867 4.5 73 106 3.05 47 960 1 1300 4.8 86 101 4.10 35 7.170 1.1 67 77 2.86 66 581 6.365 4.55 1.9 82 103 50 1078 6.983 6.6 77 46 1.95 50 405 6.005 6.4 85 40 1.21 58 579 6.361 2.33 6.4 59 85 63 550 6.310 8.8 78 72 3.20 56 651 6.478 TABLE 13.14 The Liver Operation Survival Time Data: The Validatilon Data Set OS SurvTimeV In y х х, 7.1 х х, х. х, х, х, y 23 78 1.93 45 302 5.710 4.9 66 91 3.05 34 767 6.642 6.4 90 35 1.06 39 487 6.188 5.7 35 70 2.13 68 242 5.489 6.1 42 69 2.25 70 705 6.558 8.0 27 83 2.03 127 35 716 6.574 6.8 34 51 44 266 5.583 4.7 63 36 1.71 36 361 5.889 7.0 47 67 1.60 54 460 6.131 6.7 69 65 2.91 61 1060 6.966 6.7 46 78 3.26 50 502 6.219 5.8 60 86 3.11 57 882 6.782 6.7 56 32 1.53 69 352 5.864 6.8 51 58 2.18 45 307 5.727 7.2 95 82 4.68 62 1227 7.112 7.4 52 67 3.28 53 S08 6.230 5.3 53 62 242 39 419 6.038 3.5 58 84 1.74 42 536 6.294 6.8 74 79 2.25 36 902 6.805 4.4 47 49 2.42 35 189 5.242 7.0 118 4.69 59 1433 7.269 6.7 61 57 3.87 66 815 6.703 5.6 75 103 3.11 57 1144 7.042 6.9 58 88 3.46 37 571 6.347 6.2 62 57 1.25 53 591 6.382 4.7 97 27 1.77 36 $33 6.279 6.8 69 60 2.90 56 534 6.280 6.0 73 58 1.22 36 374 5.924 5.9 50 62 3.19 69 222 5.403 5.5 88 74 3.21 36 881 6.781 3.8 55 52 1.41 69 470 6.153 4.3 99 83 3.93 35 913 6.817 6.6 48 54 2.94 59 527 6.267 6.2 42 63 1.85 32 676 6.516 5.0 60 105 3.17 34 850 6.745 5.8 62 82 3.18 45 569 6.344 5.2 56 49 1.48 54 182 5.204 5.7 70 59 2.28 65 421 6.043 4.7 64 48 1.30 56 245 5.501 7.8 74 49 2.58 33 611 6.415 4.8 52 45 2.71 63 338 5.823 4.9 72 90 3.51 45 875 6.774 4.6 73 2.82 38 750 6.620 5.9 78 70 4.28 55 935 6.841 4.6 69 70 3.17 43 583 6.368 6.1 1.84 35 319 5.765 5.9 88 98 3.33 36 1158 7.054 4.7 66 68 1.80 35 553 6.315 10.4 62 4.65 50 1041 6.948 5.8 70 64 2.52 49 589 6.378 5.4 64 81 1.36 62 599 6.395 6.9 90 33 2.78 48 655 6.485 7.9 45 55 2.46 43 377 5.932 4.5 68 60 2.07 59 642 6.465