Consider the function and the unit vector Does the directional derivative of at P(0, 0) in the direction of u exist? If (0, 0)

Consider the function

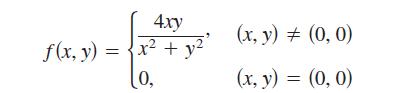
and the unit vector

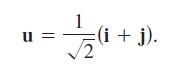
Does the directional derivative of ƒ at P(0, 0) in the direction of
u exist? If ƒ(0, 0) were defined as 2 instead of 0, would the
directional derivative exist?

f(x, y) 4xy x + y 0, (x, y) = (0, 0) (x, y) = (0, 0)