In order to build a highway, it is necessary to fill a section of a valley where the grades (slopes) of the sides are 9% and 6% (see figure). The top of the filled region will have the shape of a parabolic arc that is tangent to the two slopes at the points A and B. The horizontal distances from A to the y-axis and from B to the y-axis are both 500 feet.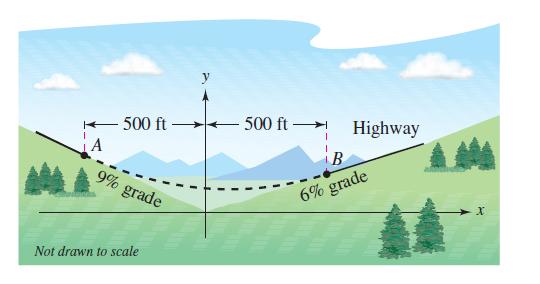(a) Find the coordinates of A and B.

(b) Find a quadratic function y = ax² + bx + c for -500 ≤ x ≤ 500 that describes the top of the filled region.

(c) Construct a table giving the depths d of the fill for x = -500, -400, -300, -200, -100, 0, 100, 200, 300, 400, and 500.

(d) What will be the lowest point on the completed highway?
Will it be directly over the point where the two hillsides
come together?

Transcribed Image Text:

A 500 ft →→→→500 ft 9% grade y Not drawn to scale Highway B 6% grade X