Prove the identity, where R is a simply connected region with boundary C. Assume that the required
Question:
Prove the identity, where R is a simply connected region with boundary C. Assume that the required partial derivatives of the scalar functions ƒ and g are continuous. The expressions DNƒ and DNg are the derivatives in the direction of the outward normal vector N of C, and are defined by DNƒ = ∇ƒ . N, and DNg = ∇g . N.
Green’s first identity:
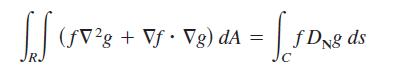
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





