Repeat Exercise 93 for which the exact solution of the differential equation where y(0) = 1, is
Question:
Repeat Exercise 93 for which the exact solution of the differential equation
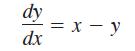
where y(0) = 1, is y = x - 1 + 2e-x.
Data from in Exercises 93
The exact solution of the differential equation
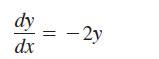
where y(0) = 4, is y = 4e-2x.
(a) Use a graphing utility to complete the table, where y is the exact value of the solution, y1 is the approximate solution using Euler's Method with h = 0.1, y2 is the approximate solution using Euler's Method with h = 0.2, e1 absolute error |y - y₁|, e2 is the absolute error |y - y₁|, and r is the ratio e1/e2.
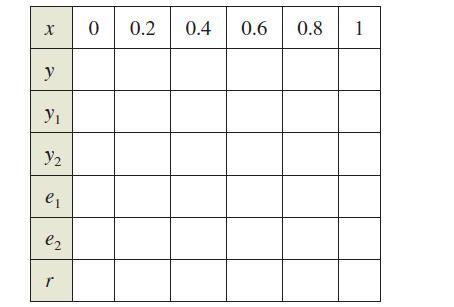
(b) What can you conclude about the ratio r as h changes?
(c) Predict the absolute error when h = 0.05.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





