Evaluate the integral in terms of the constants. Prove a famous result of Archimedes (generalizing Exercise 50): For r

(a) Show that C has x-coordinate (r + s)/².

(b) Show that ABDE has area (s − r)^3/4 by viewing it as a parallelogram of height s − r and base of length CF.

(c) Show that ACE has area (s − r)^3/8 by observing that it has the same base and height as the parallelogram.

(d) Compute the shaded area as the area under the graph minus the area of a trapezoid, and prove Archimedes’s result.

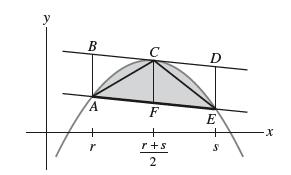
Data From Exercise 50

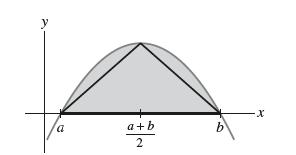
Show that the area of the shaded parabolic arch in Figure 6 is equal to four-thirds the area of the triangle shown.

Transcribed Image Text:

y B A r с F + r+s 2 D E + S -X