Figure 6 shows the geometry behind the derivative formula (sin )= cos . Segments BA and BD
Question:
Figure 6 shows the geometry behind the derivative formula (sin θ)= cos θ. Segments BA and BD are parallel to the x- and y-axes. Let Δ sin θ = sin(θ + h) − sin θ. Verify the following statements:
(a) Δ sin θ = BC
(b) ∠BDA = θ Hint: O̅A̅ ⊥ AD.
(c) BD = (cos θ)AD
Now explain the following intuitive argument: If h is small, then BC ≈ BD and AD ≈ h, so Δ sin θ ≈ (cos θ)h and (sin θ)'= cos θ.
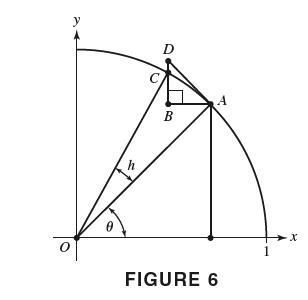
Transcribed Image Text:
y h D B A FIGURE 6 1 X
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 66% (3 reviews)
a We note that sin0 h is the ycoordinate of the point C a...View the full answer

Answered By

Irfan Ali
I have a first class Accounting and Finance degree from a top university in the World. With 5+ years experience which spans mainly from the not for profit sector, I also have vast experience in preparing a full set of accounts for start-ups and small and medium-sized businesses. My name is Irfan Ali and I am seeking a wide range of opportunities ranging from bookkeeping, tax planning, business analysis, Content Writing, Statistic, Research Writing, financial accounting, and reporting.
4.70+
249+ Reviews
530+ Question Solved
Related Book For 

Question Posted:
Students also viewed these Mathematics questions
-
Figure 6 shows the contour map for a hill 60 feet high, which we assume has equation z = ((x, y). (a) A raindrop landing on the hill above point. A will reach the xy-plane at A( by following the path...
-
Figure 6 shows the quarterly sales of Cisco Systems from 1Q:1991 to 4Q:2000. FIGURE 6 Quarterly Sales at Cisco Table 6 gives the regression statistics from estimating the model Îln (Sales t) =...
-
Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...
-
- Conducting a case analysis that deals directly with consumer behavior in a contemporary context. - Choose a company/brand or organization that is of interest to you. All companies and organizations...
-
Salvador, Inc. reported net income of $2.5 million in 2008. Depreciation for the year was $260,000, accounts receivable decreased $350,000, and accounts payable decreased $280,000. Compute net cash...
-
Suppose that the average household in a state consumes 800 gallons of gasoline per year. A 20-cent gasoline tax is introduced, coupled with a $160 annual tax rebate per household. Will the household...
-
Why might a manager close to retirement select a higher debt ratio than a manager far from retirement? AppendixLO1
-
Nicole Lawrence opened a business called Nickies Neat Ideas in January 20--. Set up T accounts for the following accounts: Cash; Accounts Receivable; Office Supplies; Computer Equipment; Office...
-
Apple Hilly Farms Ned Hilly was an investment banker and worked in San Francisco at a large bank. As retirement got closer his wife, Sally, and him decided to spend their retirement up in the Sierra...
-
I attached the entire code but the only parts that need to be fixed are the def calc_movie_feature_matrix in class ContentBased, calc_item_item_similarity in class ContentBased, and predict_from_sim...
-
Let (x) = g(x) = x. Show that ( /g)' ' /g'.
-
Use implicit differentiation to calculate higher derivatives. Use the method of the previous exercise to compute y" at the point (1, 1) on the curve x 3 + y 3 = 3x + y 2. Data From Exercise 61...
-
Many of the early barnstormers a. were in favor of the Air Commerce Act of 1926. b. were ex-World War I pilots. c. held licenses issued by Bureau of Air Commerce. d. were ex-Post Office Department...
-
Marcus expresses an interest in learning more about Katie's job position, telling her that he hopes to be in the position himself one day. Katie decides to take Marcus under her wing and teach him...
-
Losing to a Weaker Foe What began as a heavily conventional military campaign to unseat the regime of Saddam Hussein had become a bitter, unconventional struggle against frustrated Sunnis who...
-
Question A4 (12 marks) Comfort Dance Corporation (CDC) is a major distributor of dance shoes. All sales are on terms 2/10, n/30. CDC uses a perpetual inventory system. The March opening balance in...
-
7 A car rental company is interested in improving the customer experience. A data professional fixes typos and inaccuracies from a dataset containing feedback and ratings. They also verify and share...
-
CM could not believe that his company, which had once had the reputation as an industry leader in a local niche furniture market with an exciting future, could be facing bankruptcy. He wondered how...
-
The length of an algebra book is measured by many people. The measurements have mean 284 mm and standard deviation 1.3 mm. If four students measure the book, what is the probability that the mean of...
-
Select a mass spectrometric technique with the highest mass resolution for identifying an unknown compound being eluted from a liquid chromatography column
-
Object 2, with initial condition p(0) = 10.0. To find the formula for the velocities, note that they decrease linearly in time. The velocities of four objects are measured at discrete times. Use...
-
Object 3, with initial condition p(0) = 10.0. To find the formula for the velocities, compare them with the perfect square numbers. The velocities of four objects are measured at discrete times. Use...
-
Object 4, with initial condition p(0) = 10.0. The velocities follow a quadratic equation of the form v(t) = t2/2 + at + b for some value of a. The velocities of four objects are measured at discrete...
-
Alpha Technology's work in process inventory on June 1 has a balance of $27,200 representing Job No. 72. During June, $68,900 of direct materials were requisitioned for Job No. 72 and $5,500 of...
-
Retained Earnings, Beginning Balance $600,000 Common Stock-no par: Beginning Balance 248,000 Net Income 89,000 Dividends Declared (23,000) Unrealized Gain on Available-for-Sale Investments-Net of tax...
-
Hill Industries had sales in 2019 of $7,520,000 and gross profit of $1,233,000. Management is considering two alternative budget plans to increase its gross profit in 2020. Plan A would increase the...

Study smarter with the SolutionInn App


