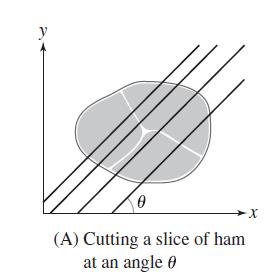
Figure 8(A) shows a slice of ham Prove that for any angle (0 ), it is possible to cut the slice in half with a cut of incline The lines of inclination are given by the equations y (tan )x b, where b varies from to Each such line divides the slice into two pieces (one of which may be empty) Let A(b)...

Let be such that 0 For any b consider the line L0 drawn at angl ...

Figure 8(A) shows a slice of ham. Prove that for any angle (0

Question:

Figure 8(A) shows a slice of ham. Prove that for any angle θ (0 ≤ θ ≤ π), it is possible to cut the slice in half with a cut of incline θ. The lines of inclination θ are given by the equations y = (tan θ)x + b, where b varies from −∞ to ∞. Each such line divides the slice into two pieces (one of which may be empty). Let A(b) be the amount of ham to the left of the line minus the amount to the right, and let A be the total area of the ham. Show that A(b) = −A if b is sufficiently large and A(b) = A if b is sufficiently negative. Then use the IVT. This works if θ ≠ 0 or π/2. If θ = 0, define A(b) as the amount of ham above the line y = b minus the amount below. How can you modify the argument to work when θ = π/2 (in which case tan θ = ∞)?

0 (A) Cutting a slice of ham at an angle X