In Section 17.1, we showed that if \(C\) is a simple closed curve, oriented counterclockwise, then the area enclosed by \(C\) is given by
\[
\text { area enclosed by } C=\frac{1}{2} \oint_{C} x d y-y d x
\]
Suppose that \(C\) is a path from \(P\) to \(Q\) that is not closed but has the property that every line through the origin intersects \(C\) in at most one point, as in Figure 7. Let \(\mathcal{R}\) be the region enclosed by \(C\) and the two radial segments joining \(P\) and \(Q\) to the origin. Show that the line integral in Eq. (1) is equal to the area of \(\mathcal{R}\).

Show that the line integral of \(\mathbf{F}=\langle-y, xangle\) along the two radial segments is zero and apply Green's Theorem.

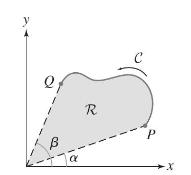
Q R P -X