Prove the following generalization of Eq. (1). Let (C) be a simple closed curve in the plane

Question:

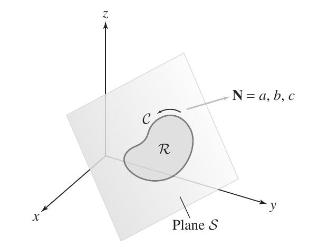
Prove the following generalization of Eq. (1). Let $C$ be a simple closed curve in the plane $\mathcal{S}$ with equation $a x+b y+c z+d=0$ (Figure 8). Then the area of the region $R$ enclosed by $C$ is equal to
\[
\frac{1}{2\|\mathbf{N}\|} \oint_{C}(b z-c y) d x+(c x-a z) d y+(a y-b x) d z
\]
where $\mathbf{N}=\langle a, b, cangle$ is the normal to $\mathcal{S}$, and $\mathcal{C}$ is oriented as the boundary of $\mathcal{R}$ (relative to the normal vector $\mathbf{N})$. Apply Stokes' Theorem to $\mathbf{F}=\langle b z-c y, c x-a z, a y-b xangle$.

image text in transcribed