Let F(x, y) = x1exy. Show that 2 F/x y = yexy and use the result

Question:

Let F(x, y) = x−1exy. Show that ∂²F/∂x ∂y = yexy and use the result of Exercise 52 to evaluate 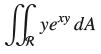SSR" yexy da for R = [1, 3] × [0, 1].

Data From Exercise 52

Prove the following extension of the Fundamental Theorem of Calculus to two variables: If ∂²F/∂x ∂y = ƒ(x, y), then

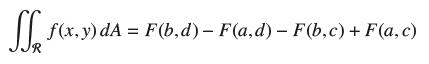
f R f(x,y) dA= F(b,d) - F(a,d) - F(b,c) + F(a, c)

where R = [a, b] × [c, d].

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Calculus

ISBN: 9781319055844

4th Edition

Authors: Jon Rogawski, Colin Adams, Robert Franzosa

See More Books

Question Posted: Jan 17, 2024 03:03 AM

What revenue categories do you think needs to be added to the master chart of accounts to reflect the new economy?
Imagine that you have samples of the following four isomeric amines, but you dont know which is which. Explainhow you could use proton NMR to distinguish among them. NH PhCHCHCH3 A NH I PhCHCHCH3 C...
(f) Emery paid $1,200 cash on April 1, 20X1 for 12 months of insurance expense and recorded it as an asset. Type- Date Why - Account Name PR Debit Credit g) Emery performed services worth $2,000 on...
The administrator of Hope Hospital has been asked to perform an activity analysis of the emergency room (ER). The ER activities include cost of quality and other patient care activities. The lab...
A particle of mass m whose total energy is twice its rest energy collides with an identical particle at rest. If they stick together, what is the mass of the resulting composite particle? What is its...
How does the sense of touch influence consumers reactions to products?
On January 1, 2008, a company agrees to pay $20,000 in three years. If the annual interest rate is 10%, determine how much cash the company can borrow with this agreement. AppendixLO1
Using the information presented in the following table, identify the processing sequence that would result using (1) FCFS, (2) SPT, (3) EDD, and (4) CR. For each method, determine (1) average job...
QUESTION 21 Bayside Company reported a net loss of $8,000 for the year ended December 31, 2019. During the year, accounts receivable increased $15,000, merchandise inventory decreased $20,000,...
Find a function F(x, y) satisfying and use the result of Exercise 52 to evaluate for R = [0, 1] [0, 4]. Data From Exercise 52 Prove the following extension of the Fundamental Theorem of Calculus to...
Prove the following extension of the Fundamental Theorem of Calculus to two variables: If 2 F/x y = (x, y), then where R = [a, b] [c, d]. R f(x,y) dA= F(b,d) - F(a,d) - F(b,c) + F(a, c)
What do you mean by marginal costing? Discuss its usefulness and limitations.
Fineas Co. use the Job Order Costing system to determine product costs. Before entering 2020, the company has created a production budget, with an estimated total manufacturing overhead of $...
Define what a market value is? What are three major principles of investing funds? How does the federal government control the money supply? An investor purchases a 10-year U.S. Treasury note and...
1. Suppose we have two alternative designs, each of which yields a different present value of the total lifetime cost: the first is $1604 and the second is $1595. Verify that the present value of the...
Sometimes when we are asked for a linear model, the information that we are given is data about a scenario. In these cases we have to use Excel to generate a trendline. There is a video in this...
1. Purpose Explain 3 points from the Introduction section as to why this study is important. How did this study build on the existing literature in this area? 2. Participants Outline at least 2...
Octane, C8H18, is burned with 150% theoretical air, determine the (a) Molar analysis of the products of combustion. (b) The dew point of the products if the pressure is 0.1 MPa.
Suppose the concentration of glucose inside a cell is 0.1 mm and the cell is suspended in a glucose solution of 0.01 mm. a. What would be the free energy change involved in transporting 10-o mole of...
Solve the equation. 25x 2 + 16 = 40x
Solve the equation. x + 12/x = 7
Solve the equation. 4( 2) 3 3 -3 x( 3)
How does the life time analysis differ from the basic customer profitability approach(500 words)
The security analysis research reports, published by sell side analysts working for security firms and FINRA, purport to sell an analyst's investment ideas to an investor in exchange for...
During the month of September,the Cider Pressing Company is trying to determine how much cider they are going to sell in October and November. One gallon of cider typically sells for $7 per gallon....

Let F(x, y) = x1exy. Show that 2 F/x y = yexy and use the result

Question:

SSR" yexy da

Step by Step Answer:

Differentiating Fx y xey with respect to y gives F xlery dy y We no...View the full answer

Calculus

Students also viewed these Mathematics questions