Let (f(x, y)=x+frac{x}{x^{2}+y^{2}}). The vector field (mathbf{F}=abla f) (Figure 5) provides a model in the plane of
Question:
Let \(f(x, y)=x+\frac{x}{x^{2}+y^{2}}\). The vector field \(\mathbf{F}=abla f\) (Figure 5) provides a model in the plane of the velocity field of an incompressible, irrotational fluid flowing past a cylindrical obstacle (in this case, the obstacle is the unit circle \(x^{2}+y^{2}=1\) ).
(a) Verify that \(\mathbf{F}\) is irrotational [by definition, \(\mathbf{F}\) is irrotational if \(\operatorname{curl}(\mathbf{F})=\mathbf{0}\) ].
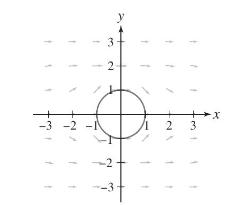
(b) Verify that \(\mathbf{F}\) is tangent to the unit circle at each point along the unit circle except \((1,0)\) and \((-1,0)\) (where \(\mathbf{F}=\mathbf{0}\) ).
(c) What is the circulation of \(\mathbf{F}\) around the unit circle?
(d) Calculate the line integral of \(\mathbf{F}\) along the upper and lower halves of the unit circle separately.
Step by Step Answer:






