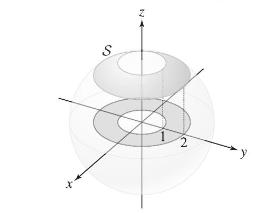
Let (mathcal{S}) be the portion of the sphere (x^{2}+y^{2}+z^{2}=9), where (1 leq x^{2}+y^{2} leq 4) and (z

Question:

Let $\mathcal{S}$ be the portion of the sphere $x^{2}+y^{2}+z^{2}=9$, where $1 \leq x^{2}+y^{2} \leq 4$ and $z \geq 0$ (Figure 20). Find a parametrization of $S$ in polar coordinates and use it to compute:
(a) The area of $\mathcal{S}$
(b) $\iint_{\mathcal{S}} z^{-1} d S$

S N