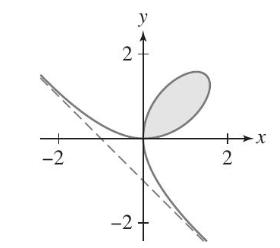
Let (x^{3}+y^{3}=3 x y) be the folium of Descartes (Figure 22). (a) Show that the folium has

Question:

Let $x^{3}+y^{3}=3 x y$ be the folium of Descartes (Figure 22).
(a) Show that the folium has a parametrization in terms of $t=y / x$ given by
\[
x=\frac{3 t}{1+t^{3}}, \quad y=\frac{3 t^{2}}{1+t^{3}} \quad(-\infty\]
(b) Show that
\[
x d y-y d x=\frac{9 t^{2}}{\left(1+t^{3}ight)^{2}} d t
\]

By the Quotient Rule,

\[
x^{2} d\left(\frac{y}{x}ight)=x d y-y d x
\]
(c) Find the area of the loop of the folium. The limits of integration are 0 and $\infty$.

image text in transcribed