Prove that if a planetary orbit is circular of radius R, then vT = 2R, where v

Prove that if a planetary orbit is circular of radius R, then vT = 2πR, where v is the planet’s speed (constant by Exercise 7) and T is the period. Then use Kepler’s Third Law to prove that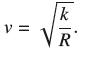

Data From Exercise 7

Show that a planet in a circular orbit travels at constant speed. Use the facts that J is constant and that r(t) is orthogonal to'(t) for a circular orbit.

Transcribed Image Text:

V= k R