Find the velocity of a satellite in geosynchronous orbit about the earth. Use Exercises 6 and 9.
Question:
Find the velocity of a satellite in geosynchronous orbit about the earth. Use Exercises 6 and 9.
Data From Exercise 6
A satellite orbiting above the equator of the earth is geosynchronous if the period is T = 24 hours (in this case, the satellite stays over a fixed point on the equator). Use Kepler’s Third Law to show that in a circular geosynchronous orbit, the distance from the center of the earth is R ≈ 42,246 km. Then compute the altitude h of the orbit above the earth’s surface. The earth has mass M ≈ 5.974 × 1024 kg and radius R ≈ 6371 km.
Data From Exercise 9
Prove that if a planetary orbit is circular of radius R, then vT = 2πR, where v is the planet’s speed (constant by Exercise 7) and T is the period. Then use Kepler’s Third Law to prove that 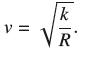
Step by Step Answer:






