(a) Use cylindrical coordinates to show that the volume of the solid bounded above by the sphere r² + z² = a² and below by the cone z = r cot Φ₀ (or Φ = Φ₀), where 0 < Φ₀ < π/2, is

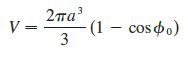
(b) Deduce that the volume of the spherical wedge given by ρ₁ ≤ ρ ≤ ρ₂, θ₁ ≤ θ ≤ θ₂, Φ₁ ≤ Φ ≤ Φ₂ is

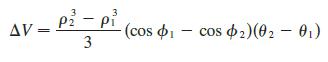
(c) Use the Mean Value Theorem to show that the volume in part (b) can be written as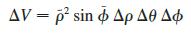

where ρ̃ lies between ρ₁ and ρ₂, Φ̃ lies between Φ₁ and Φ₂, Δρ = ρ₂ − ρ₁, Δθ = θ₂ − θ₁, and ΔΦ = Φ₂ − Φ₁.

Transcribed Image Text:

2ma V = (1 cos oo) 3