Let a_n = (1 + 1/n)n.

(a) Show that if 0 ≤ a < b, then

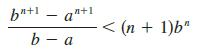
(b) Deduce that bⁿ[(n + 1)a − nb], aⁿ⁺¹.

(c) Use a = 1 + 1/(n + 1) and b = 1 + 1/n in part (b) to show that {an} is increasing.

(d) Use a = 1 and b = 1 + 1/(2n) in part (b) to show that a_2n < 4.

(e) Use parts (c) and (d) to show that a_n < 4 for all n.

(f) Use Theorem 12 to show that lim_n→∞(1 + 1/n)ⁿ exists.

Transcribed Image Text:

b"+l - a"+1 a*+1 b — а < (п + 1)b"