Let S be a smooth parametric surface and let P be a point such that each line that starts at P intersects S at most once. The solid angle Ω(S) subtended by S at P is the set of lines starting at P and passing through S. Let S(a) be the intersection of Ω(S) with the surface of the sphere with center P and radius a. Then the measure of the solid angle (in steradians) is defined to be

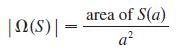
Apply the Divergence Theorem to the part of Ω(S) between S(a) and S to show that

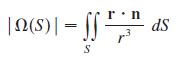
where r is the radius vector from P to any point on S, r = |r|, and the unit normal vector n is directed away from P. This shows that the definition of the measure of a solid angle is independent of the radius a of the sphere. Thus the measure of the solid angle is equal to the area subtended on a unit sphere. The total solid angle subtended by a sphere at its center is thus 4π steradians.

Transcribed Image Text:

area of S(a) a? 2(S)\