A Lorenz curve is given by y = L(x), where 0 ≤ x ≤ 1 represents the lowest fraction of the population of a society in terms of wealth and 0 ≤ y ≤ 1 represents the fraction of the total wealth that is owned by that fraction of the society. For example, the Lorenz curve in the figure shows that L(0.5) = 0.2, which means that the lowest 0.5 (50%) of the society owns 0.2 (20%) of the wealth. (See the Guided Project Distribution of Wealth for more on Lorenz curves.)

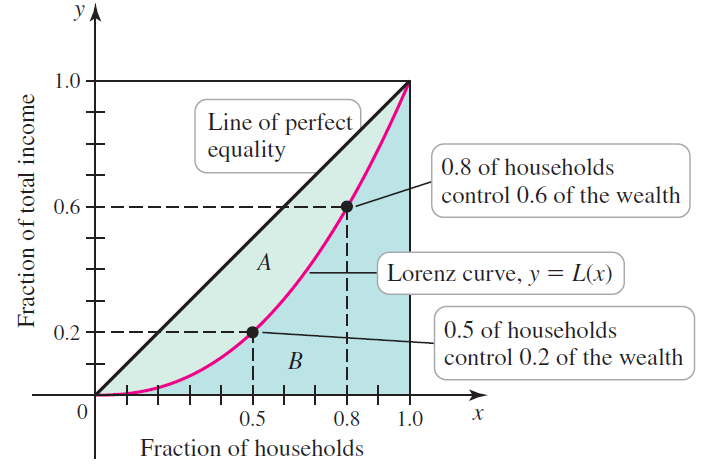
a. A Lorenz curve y = L(x) is accompanied by the line y = x, called the line of perfect equality. Explain why this line is given this name.

b. Explain why a Lorenz curve satisfies the conditions L(0) = 0, L(1) = 1, L(x) ≤ x, and L'(x) ≥ 0 on [0, 1].

c. Graph the Lorenz curves L(x) = x^p corresponding to p = 1.1, 1.5, 2, 3, 4. Which value of p corresponds to the most equitable distribution of wealth (closest to the line of perfect equality)? Which value of p corresponds to the least equitable distribution of wealth? Explain. 

d. The information in the Lorenz curve is often summarized in a single measure called the Gini index, which is defined as follows. Let A be the area of the region between y = x and y = L(x) (see figure) and let B be the area of the region between y = L(x) and the x-axis. Then the Gini index is

e. Compute the Gini index for the cases L(x) = x^p and p = 1.1, 1.5, 2, 3, 4.

f. What is the smallest interval [a, b] on which values of the Gini index lie for L(x) = x^p with p ≥ 1? Which endpoints of [a, b] correspond to the least and most equitable distribution of wealth?

g. Consider the Lorenz curve described by L(x) = 5x^2/6 + x/6. Show that it satisfies the conditions L(0) = 0, L(1) = 1, and L'(x) ≥ 0 on [0, 1]. Find the Gini index for this function.

Transcribed Image Text:

УА 1.0 Line of perfect equality 0.8 of households control 0.6 of the wealth 0.6 - Lorenz curve, y = L(x) 0.5 of households 0.2 control 0.2 of the wealth B х 0.5 0.8 1.0 Fraction of households Fraction of total income .1 G = A + B' Show that G 2A = 1 – 2 L(x) dx.