Suppose a dartboard occupies the square {(x, y): 0 ≤ |x| ≤ 1, 0 ≤ |y| ≤ 1}. A dart is thrown randomly at the board many times (meaning it is equally likely to land at any point in the square). What fraction of the dart throws land closer to the edge of the board than the center? Equivalently, what is the probability that the dart lands closer to the edge of the board than the center? Proceed as follows.

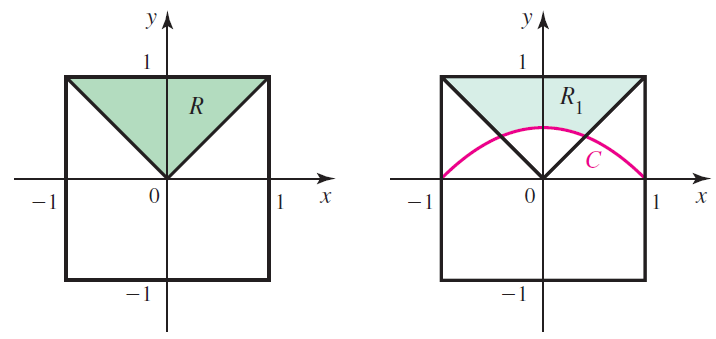
a. Argue that by symmetry, it is necessary to consider only one quarter of the board, say the region R: {(x, y): |x| ≤ y ≤ 1}.

b. Find the curve C in this region that is equidistant from the center of the board and the top edge of the board (see figure).

c. The probability that the dart lands closer to the edge of the board than the center is the ratio of the area of the region R₁ above C to the area of the entire region R. Compute this probability.

Transcribed Image Text:

УА УА R1 х х -1 1 -1