An infinite product P = a 1 a 2 a 3 . . , which is denoted

Question:

An infinite product P = a₁ a₂ a₃ . . , which is denoted 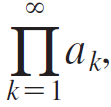По ак k=1 is the limit of the sequence of partial products {a₁, a₁ a₂, a₁ a₂ a₃, . . .}. Assume that a_k > 0 for all k.

a. Show that the infinite product converges (which means its sequence of partial products converges) provided the series 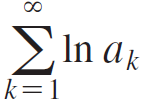Σ In ak k=1 converges.

b. Consider the infinite product

Write out the first few terms of the sequence of partial products,

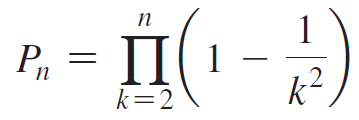
(for example, P₂ = 3/4, P₃ = 2/3). Write out enough terms to determine the value of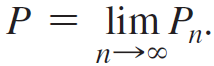

c. Use the results of parts (a) and (b) to evaluate the series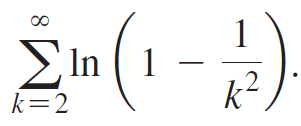

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For answer-question

Calculus Early Transcendentals

ISBN: 978-0321947345

2nd edition

Authors: William L. Briggs, Lyle Cochran, Bernard Gillett

See More Books

Question Posted: Apr 13, 2019 09:55 AM

See More Questions

Use the ideas of Exercise 88 to evaluate the following infinite products. a. b. = ee!/2 el/4 e!/8.. k=0 1 2 3 4 k 2 3 4 5 k=2
Find the remainder in the Taylor series centered at the point a for the following functions. Then show that for all x in the interval of convergence. f(x) = cos x, a = /2 lim R(x) = 0
Find the nth-order Taylor polynomial for the following functions centered at the given point a. f(x) = cos x, n = 2, a = /4
MAX DIVISOR TREE Let a tree exists with the root value N. The property of this tree is that each of its nodes branches out to the nodes with a value equal to one of its divisors (except 1 and the...
Under what conditions would you have a nor-pressure distribution in forging a solid cylindrical work piece as shown in the accompanying figure? Explain.
A heat exchanger consists of a closed system with a series of parallel tubes connected by 180 elbows as shown in the figure. There are a total of 14 return elbows. The pipe diameter is 2 cm, and the...
Use the same facts as problem 20 and prepare entries using the following independent assumptions: a. Lease A is abandoned in 2022. b. Lease A is proved in 2022. c. Insignificant Lease Y, with a cost...
If the indirect costs for each duration are $300 for 27 weeks, $240 for 26 weeks, $180 for 25 weeks, $120 for 24 weeks, $60 for 23 weeks, and $50 for 22 weeks, compute the direct, indirect and total...
How might actions/events in other countries outside the U.S. effect the aggregate supply or aggregate demand in the U.S.? Be sure to explain.
Refer to P 2-3 and complete the following steps: In P 2-3 Pastina Company sells various types of pasta to grocery chains as private label brands. The company's fiscal year-end is December 31. The...
Use the Ratio Test to determine the values of x 0 for which each series converges. 2k k=1
Working in the early 1600s, the mathematicians Wallis, Pascal, and Fermat were calculating the area of the region under the curve y = x p between x = 0 and x = 1, where p is a positive integer. Using...
The Asian Development Bank reported that Myanmars GDP growth accelerated to 7.5% in 2013 from 7.3% in 2012. Growth was supported by rising investment, improved business confidence, commodity exports,...
Carotenoids are pigments responsible for much of the red we see in nature. For example, the bright red beak color of the male zebra finch is derived from carotenoids. Carotenoids are also important...
Refer to Assignment Problem 22. In the same study, Zahran et al. (2010) also measured the lead concentration of blood (in g/dl) of children living in the 46 areas both before and after the...
Calculation practice: Analyze results from a TukeyKramer test. Using the same data as in Practice Problem 1, use the results from a TukeyKramer test to illustrate which of the pairs of groups are...
Fill in the blanks: Year 1970 1980 1990 2000 2010 2020 2030 Real GDP (in 2000 dollars) 3,000 5,000 10,000 20,000 Nominal GDP (in current dollars) 1,200 6,000 8,000 15,000 50,000 GDP deflator (base...
The accompanying diagram shows the interest rate on one-year loans and inflation during 19982013 in the economy of Albernia. When would one-year loans have been especially attractive and why?...
How might a leader modify the clothing he or she wore to different work situations to help practice contingency leadership?
A city maintains a solid waste landfill that was 12 percent filled at the end of Year 1 and 26 percent filled at the end of Year 2. During those periods, the government estimated that total closure...
1. Answer Problem 4.74 for bone density of the femoral neck? 2. Answer Problem 4.75 for bone density of the femoral neck?
Determine whether the underlined value is a parameter or a statistic. 1. Following the 2014 national midterm election, 18% of the governors of the 50 United States were female. 2. The average score...
A farmer interested in the weight of his soybean crop randomly samples 100 plants and weighs the soybeans on each plant? A research objective is presented. For each, identify the population and...
LaToya Limmons is the manager of the Human Resources (HR) department and Javier Jartin is the manager of the sales department for a production company headquartered in the United States but also has...
The beam AD is fixed to a rigid wall at A and is supported by props at B and C as shown in figure 1. In sections AB and BC, the flexural rigidity is EI, but in section CD the flexural rigidity is...
What is the meaning of 'framing' and how does it impact the way we negotiate? (Your own opinion)

An infinite product P = a 1 a 2 a 3 . . , which is denoted

Question:

По ак k=1 Σ In ak k=1

Step by Step Answer:

a Let Pn be the nth partial ...View the full answer

Calculus Early Transcendentals

Students also viewed these Mathematics questions