Complete the following steps to prove that when the x- and y-coordinates of a point on the
Question:
Complete the following steps to prove that when the x- and y-coordinates of a point on the hyperbola x2 - y2 = 1 are defined as cosh t and sinh t, respectively, where t is twice the area of the shaded region in the figure, x and y can be expressed as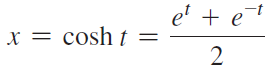 and
and 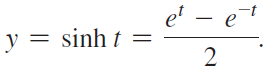
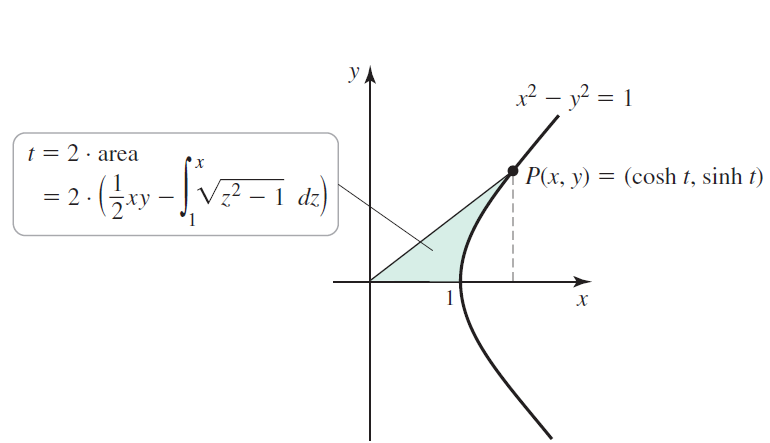
a. Explain why twice the area of the shaded region is given by
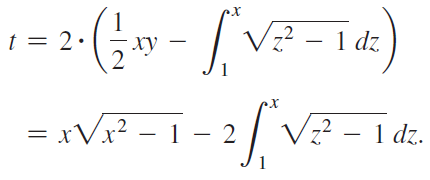
b. The formula for the integral in part (a) is derived:
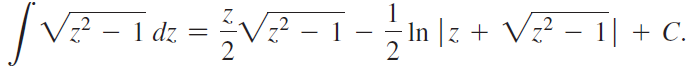
Evaluate this integral on the interval [1, x], explain why the absolute value can be dropped, and combine the result with part (a) to show that
t = ln (x + √x2 - 1).
c. Solve the final result from part (b) for x to show that
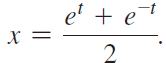
d. Use the fact that y = √x2 - 1 in combination with part (c) to show that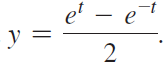
Step by Step Answer:

Calculus Early Transcendentals
ISBN: 978-0321947345
2nd edition
Authors: William L. Briggs, Lyle Cochran, Bernard Gillett





