Prove the quadrilateral property in Exercise 83, assuming the coordinates of P, Q, R, and S are P(x 1 , y 1 , 0), Q(x 2 , y 2 , 0), R(x 3 , y 3 , 0), and S(x 4 , y 4 , z 4 ), where we assume that P, Q, and R lie in the xy plane without loss of generality Data from Exercise 83 The points P, Q, R, an...

Y3Y4 Y4Y The midpoints are A2 ...

Prove the quadrilateral property in Exercise 83, assuming the coordinates of P, Q, R, and S are

Question:

Prove the quadrilateral property in Exercise 83, assuming the coordinates of P, Q, R, and S are P(x₁, y₁, 0), Q(x₂, y₂, 0), R(x₃, y₃, 0), and S(x₄, y₄, z₄), where we assume that P, Q, and R lie in the xy-plane without loss of generality.

Data from Exercise 83

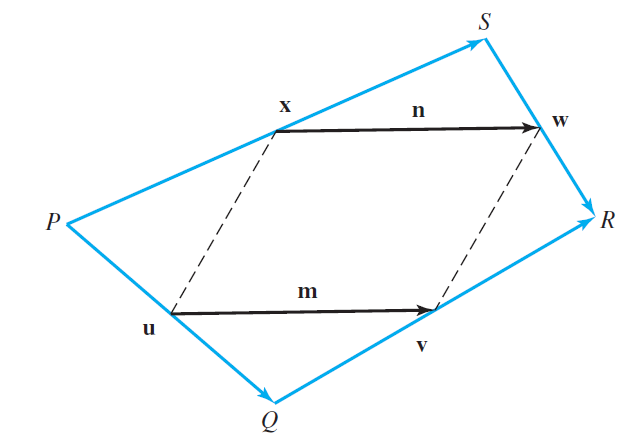
The points P, Q, R, and S, joined by the vectors u, v, w, and x, are the vertices of a quadrilateral in R³. The four points needn’t lie in a plane (see figure). Use the following steps to prove that the line segments joining the midpoints of the sides of the quadrilateral form a parallelogram. The proof does not use a coordinate system.

х n m u