The points P, Q, R, and S, joined by the vectors u, v, w, and x, are the vertices of a quadrilateral in R³. The four points needn’t lie in a plane (see figure). Use the following steps to prove that the line segments joining the midpoints of the sides of the quadrilateral form a parallelogram. The proof does not use a coordinate system.

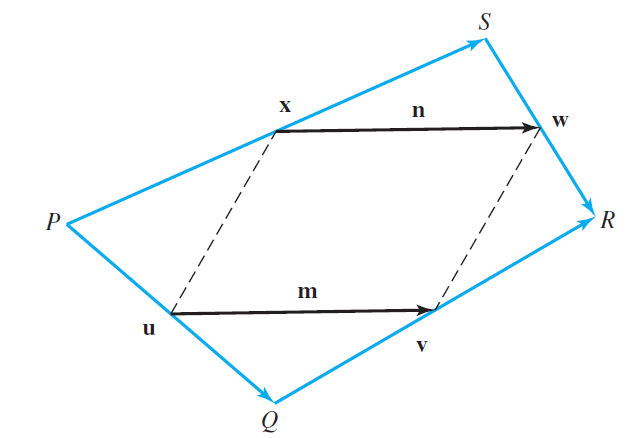
a. Use vector addition to show that u + v = w + x.

b. Let m be the vector that joins the midpoints of PQ and QR. Show that m = (u + v)/2.

c. Let n be the vector that joins the midpoints of PS and SR. Show that n = (x + w)/2.

d. Combine parts (a), (b), and (c) to conclude that m = n.

e. Explain why part (d) implies that the line segments joining the midpoints of the sides of the quadrilateral form a parallelogram.

n m u