Consider a pendulum of length L meters swinging only under the influence of gravity. Suppose the pendulum starts swinging with an initial displacement of θ₀ radians (see figure). The period (time to complete one full cycle) is given by

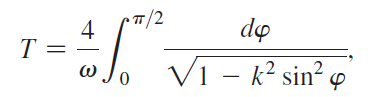
where ω² = g/L, g ≈ 9.8 m/s² is the acceleration due to gravity, and k² = sin² (θ₀/2). Assume L = 9.8 m, which means ω = 1 s^-1.

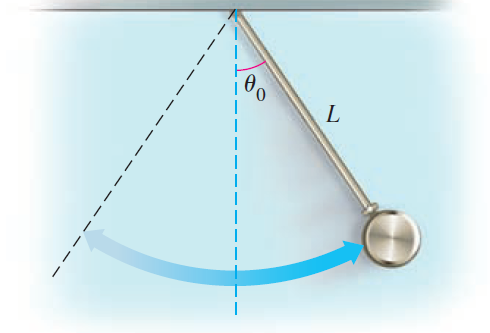
a. Use a computer algebra system to find the period of the pendulum for θ₀ = 0.1, 0.2,. . ., 0.9, 1.0 rad.

b. For small values of θ₀, the period should be approximately 2π seconds. For what values of θ₀ are your computed values within 10% of 2π (relative error less than 0.1)?

Transcribed Image Text:

п/2 do T = VI - k² sin² o