Imagine a stack of hemispherical soap bubbles with decreasing radii r₁ = 1, r₂, r₃, . . . (see figure). Let h_n be the distance between the diameters of bubble n and bubble n + 1, and let H_n be the total height of the stack with n bubbles.

a. Use the Pythagorean theorem to show that in a stack with n bubbles, h²₁ = r²₁ - r²₂ , h²₂ = r²₂ - r²₃, and so forth. Note that for the last bubble h_n = r_n.

b. Use part (a) to show that the height of a stack with n bubbles is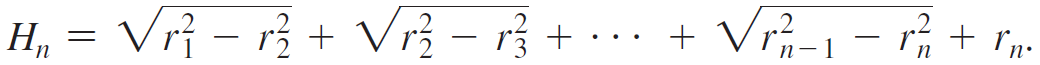

c. The height of a stack of bubbles depends on how the radii decrease. Suppose that r₁ = 1, r₂ = a, r₃ = a², . . ., r_n = a^n-1, where 0 n of a stack with n bubbles.

d. Suppose the stack in part (c) is extended indefinitely (n ??). In terms of a, how high would the stack be??

H = r} r + V r} + Hn + -1 - T + n. n- n