It can be proved that if a series converges absolutely, then its terms may be summed in
Question:
It can be proved that if a series converges absolutely, then its terms may be summed in any order without changing the value of the series. However, if a series converges conditionally, then the value of the series depends on the order of summation. For example, the (conditionally convergent) alternating harmonic series has the value
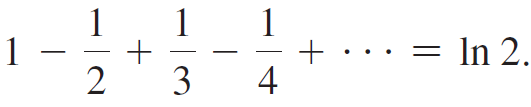
Show that by rearranging the terms (so the sign pattern is + + -),
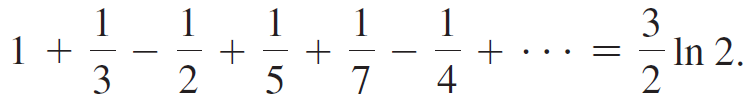
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Calculus Early Transcendentals
ISBN: 978-0321947345
2nd edition
Authors: William L. Briggs, Lyle Cochran, Bernard Gillett
Question Posted:





